| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- QA엔지니어
- 벤쿠버집구하기
- 부산입국
- 벤쿠버렌트
- FK 설정
- 외래키설정
- 파이도 환불
- Java
- 데이터의 무결성
- IntelliJ
- 백준알고리즘
- 레노보노트북
- 캐나다워홀
- 설탕문제
- database연결
- BC렌트
- 리눅스
- 언마운트
- codility
- Linux
- FIDO 환불
- 1463번
- 자바
- binaray_gap
- 프로그래머스
- FLEX5
- 엔테크서비스
- Lesson2
- 벤쿠버 렌트
- Lesson3
- Today
- Total
대충이라도 하자
Graph -chaper 1(2) 본문
Path Compression Optimization - Disjoint Set
: find function을 최적화함
***Recursion
// UnionFind.class
class UnionFind {
private int[] root;
public UnionFind(int size) {
root = new int[size];
for (int i = 0; i < size; i++) {
root[i] = i;
}
}
public int find(int x) {
if (x == root[x]) {
return x;
}
return root[x] = find(root[x]);
}
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) {
root[rootY] = rootX;
}
}
public boolean connected(int x, int y) {
return find(x) == find(y);
}
}
// App.java
// Test Case
public class App {
public static void main(String[] args) throws Exception {
UnionFind uf = new UnionFind(10);
// 1-2-5-6-7 3-8-9 4
uf.union(1, 2);
uf.union(2, 5);
uf.union(5, 6);
uf.union(6, 7);
uf.union(3, 8);
uf.union(8, 9);
System.out.println(uf.connected(1, 5)); // true
System.out.println(uf.connected(5, 7)); // true
System.out.println(uf.connected(4, 9)); // false
// 1-2-5-6-7 3-8-9-4
uf.union(9, 4);
System.out.println(uf.connected(4, 9)); // true
}
}
Optimized “disjoint set” with Path Compression and Union by Rank
// UnionFind.class
class UnionFind {
private int[] root;
// Use a rank array to record the height of each vertex, i.e., the "rank" of each vertex.
private int[] rank;
public UnionFind(int size) {
root = new int[size];
rank = new int[size];
for (int i = 0; i < size; i++) {
root[i] = i;
rank[i] = 1; // The initial "rank" of each vertex is 1, because each of them is
// a standalone vertex with no connection to other vertices.
}
}
// The find function here is the same as that in the disjoint set with path compression.
public int find(int x) {
if (x == root[x]) {
return x;
}
return root[x] = find(root[x]);
}
// The union function with union by rank
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) {
if (rank[rootX] > rank[rootY]) {
root[rootY] = rootX;
} else if (rank[rootX] < rank[rootY]) {
root[rootX] = rootY;
} else {
root[rootY] = rootX;
rank[rootX] += 1;
}
}
}
public boolean connected(int x, int y) {
return find(x) == find(y);
}
}
// App.java
// Test Case
public class App {
public static void main(String[] args) throws Exception {
UnionFind uf = new UnionFind(10);
// 1-2-5-6-7 3-8-9 4
uf.union(1, 2);
uf.union(2, 5);
uf.union(5, 6);
uf.union(6, 7);
uf.union(3, 8);
uf.union(8, 9);
System.out.println(uf.connected(1, 5)); // true
System.out.println(uf.connected(5, 7)); // true
System.out.println(uf.connected(4, 9)); // false
// 1-2-5-6-7 3-8-9-4
uf.union(9, 4);
System.out.println(uf.connected(4, 9)); // true
}
}
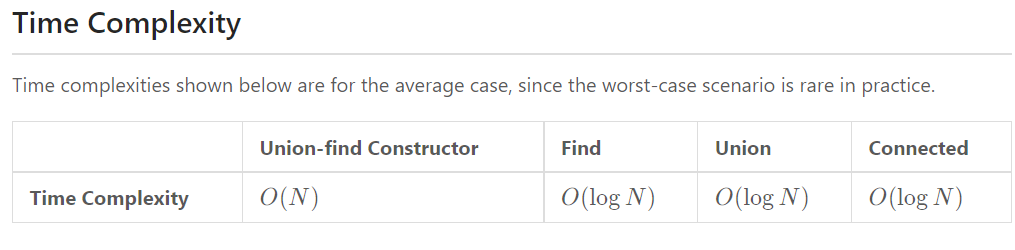
Note: N is the number of vertices in the graph. \alpha refers to the Inverse Ackermann function. In practice, we assume it's a constant. In other words, O(\alpha (N)) is regarded as O(1) on average.
- For the union-find constructor, we need to create two arrays of size N each.
- When using the combination of union by rank and the path compression optimization, the find operation will take O(\alpha(N)) time on average. Since union and connected both make calls to find and all other operations require constant time, union and connected functions will also take O(\alpha(N)) time on average.
Summary of the “disjoint set” data structure
Main idea of a disjoint set : All connected vertices have the same parent node or root node, whether directly or indirectly conntected. To check if two vertices are connected, we only need to check if they have the same root node.
The two most important functions for the “disjoint set” data structure are the find function and the union function. The find function locates the root node of a given vertex. The union function connects two previously unconnected vertices by giving them the same root node. There is another important function named connected, which checks the “connectivity” of two vertices. The find and union functions are essential for any question that uses the “disjoint set” data structure.
List of functions
public class UnionFind {
// Constructor of Union-find. The size is the length of the root array.
public UnionFind(int size) {}
public int find(int x) {}
public void union(int x, int y) {}
public boolean connected(int x, int y) {}
}Find function - basic
public int find(int x) {
while (x != root[x]) {
x = root[x];
}
return x;
}
Find function - optimized with path compression
public int find(int x) {
if (x == root[x]) {
return x;
}
return root[x] = find(root[x]);
}union function of the “disjoint set” - basic
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) {
root[rootY] = rootX;
}
}- The union function – Optimized by union by rank:
-
public void union(int x, int y) { int rootX = find(x); int rootY = find(y); if (rootX != rootY) { if (rank[rootX] > rank[rootY]) { root[rootY] = rootX; } else if (rank[rootX] < rank[rootY]) { root[rootX] = rootY; } else { root[rootY] = rootX; rank[rootX] += 1; } } }
'꼬꼬마 개발자 노트 > Coding Problems' 카테고리의 다른 글
| Array and String - Introduction to Array (0) | 2022.02.07 |
|---|---|
| Leetcode - Graph (0) | 2022.01.26 |
| Graph - Disjoint Set (0) | 2022.01.18 |
| Graph - overview (0) | 2022.01.18 |
| Arrays-chapter6 (0) | 2022.01.17 |


