| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- codility
- 1463번
- 파이도 환불
- 엔테크서비스
- binaray_gap
- 캐나다워홀
- Java
- Linux
- Lesson2
- FIDO 환불
- 리눅스
- FLEX5
- 외래키설정
- 벤쿠버렌트
- 데이터의 무결성
- 부산입국
- BC렌트
- 언마운트
- 설탕문제
- 벤쿠버집구하기
- 레노보노트북
- Lesson3
- 백준알고리즘
- 벤쿠버 렌트
- 자바
- QA엔지니어
- FK 설정
- 프로그래머스
- IntelliJ
- database연결
- Today
- Total
대충이라도 하자
Graph - Disjoint Set 본문
Note that others might refer to it as an algorithm. In this Explore Card, the term “disjoint set” refers to a data structure. The primary use of disjoint sets is to address the connectivity between the components of a network. The “network“ here can be a computer network or a social network. For instance, we can use a disjoint set to determine if two people share a common ancestor.
- Parent node: the direct parent node of a vertex. For example, in Figure 5, the parent node of vertex 3 is 1, the parent node of vertex 2 is 0, and the parent node of vertex 9 is 9.
- Root node: a node without a parent node; it can be viewed as the parent node of itself. For example, in Figure 5, the root node of vertices 3 and 2 is 0. As for 0, it is its own root node and parent node. Likewise, the root node and parent node of vertex 9 is 9 itself. Sometimes the root node is referred to as the head node.
-> Check if two nodes are connected -> Find the head of the node. If they have same head of the node, it means they are connected
The two important functions of a “disjoint set.”
In the introduction videos above, we discussed the two important functions in a “disjoint set”.
- The find function finds the root node of a given vertex. For example, in Figure 5, the output of the find function for vertex 3 is 0.
- The union function unions two vertices and makes their root nodes the same. In Figure 5, if we union vertex 4 and vertex 5, their root node will become the same, which means the union function will modify the root node of vertex 4 or vertex 5 to the same root node.
There are two ways to implement a “disjoint set”.
Implementation with Quick Find: in this case, the time complexity of the find function will be O(1). However, the union function will take more time with the time complexity of O(N).
- Implementation with Quick Union: compared with the Quick Find implementation, the time complexity of the union function is better. Meanwhile, the find function will take more time in this case.
1. Quick Find
// UnionFind.class
class UnionFind {
private int[] root;
public UnionFind(int size) {
root = new int[size];
for (int i = 0; i < size; i++) {
root[i] = i;
}
}
public int find(int x) {
return root[x];
}
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) {
for (int i = 0; i < root.length; i++) {
if (root[i] == rootY) {
root[i] = rootX;
}
}
}
}
public boolean connected(int x, int y) {
return find(x) == find(y);
}
}
// App.java
// Test Case
public class App {
public static void main(String[] args) throws Exception {
UnionFind uf = new UnionFind(10);
// 1-2-5-6-7 3-8-9 4
uf.union(1, 2);
uf.union(2, 5);
uf.union(5, 6);
uf.union(6, 7);
uf.union(3, 8);
uf.union(8, 9);
System.out.println(uf.connected(1, 5)); // true
System.out.println(uf.connected(5, 7)); // true
System.out.println(uf.connected(4, 9)); // false
// 1-2-5-6-7 3-8-9-4
uf.union(9, 4);
System.out.println(uf.connected(4, 9)); // true
}
}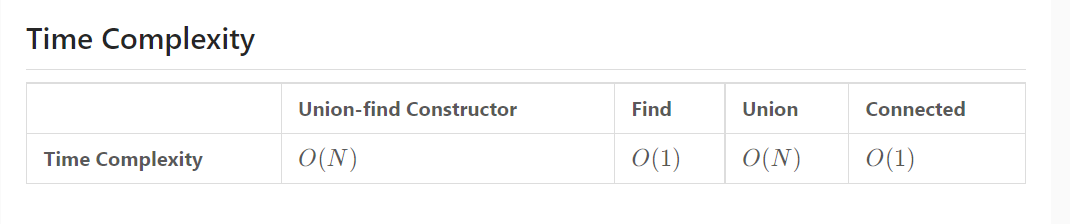
Note: N is the number of vertices in the graph.
- When initializing a union-find constructor, we need to create an array of size N with the values equal to the corresponding array indices; this requires linear time.
- Each call to find will require O(1) time since we are just accessing an element of the array at the given index.
- Each call to union will require O(N) time because we need to traverse through the entire array and update the root vertices for all the vertices of the set that is going to be merged into another set.
- The connected operation takes O(1) time since it involves the two find calls and the equality check operation.
결국, Totally O(N)
2. Quick Union
class UnionFind {
private int[] root;
public UnionFind(int size) {
root = new int[size];
for (int i = 0; i < size; i++) {
root[i] = i;
}
}
public int find(int x) {
while (x != root[x]) {
x = root[x];
}
return x;
}
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) {
root[rootY] = rootX;
}
}
public boolean connected(int x, int y) {
return find(x) == find(y);
}
}
// App.java
// Test Case
public class App {
public static void main(String[] args) throws Exception {
UnionFind uf = new UnionFind(10);
// 1-2-5-6-7 3-8-9 4
uf.union(1, 2);
uf.union(2, 5);
uf.union(5, 6);
uf.union(6, 7);
uf.union(3, 8);
uf.union(8, 9);
System.out.println(uf.connected(1, 5)); // true
System.out.println(uf.connected(5, 7)); // true
System.out.println(uf.connected(4, 9)); // false
// 1-2-5-6-7 3-8-9-4
uf.union(9, 4);
System.out.println(uf.connected(4, 9)); // true
}
}
Generally speaking, Quick Union is more efficient than Quick Find.
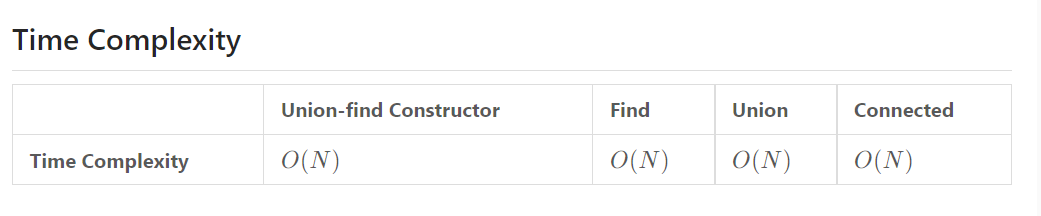
- For the find operation, in the worst-case scenario, we need to traverse every vertex to find the root for the input vertex. The maximum number of operations to get the root vertex would be no more than the tree's height, so it will take O(N) time.
- The union operation consists of two find operations which (only in the worst-case) will take O(N) time, and two constant time operations, including the equality check and updating the array value at a given index. Therefore, the union operation also costs O(N) in the worst-case.
- The connected operation also takes O(N) time in the worst-case since it involves two find calls.
Specifically, the quick find implementation will always spend O(n) time on the union operation and in the quick union implementation, as shown in Figure 1, it is possible for all the vertices to form a line after connecting them using union, which results in the worst-case scenario for the find function. Is there any way to optimize these implementations?
Of course, there is; it is to union by rank. The word “rank” means ordering by specific criteria. Previously, for the union function, we always chose the root node of x and set it as the new root node for the other vertex. However, by choosing the parent node based on certain criteria (by rank), we can limit the maximum height of each vertex.
To be specific, the “rank” refers to the height of each vertex. When we union two vertices, instead of always picking the root of x (or y, it doesn't matter as long as we're consistent) as the new root node, we choose the root node of the vertex with a larger “rank”. We will merge the shorter tree under the taller tree and assign the root node of the taller tree as the root node for both vertices. In this way, we effectively avoid the possibility of connecting all vertices into a straight line. This optimization is called the “disjoint set” with union by rank.
// UnionFind.class
class UnionFind {
private int[] root;
private int[] rank;
public UnionFind(int size) {
root = new int[size];
rank = new int[size];
for (int i = 0; i < size; i++) {
root[i] = i;
rank[i] = 1;
}
}
public int find(int x) {
while (x != root[x]) {
x = root[x];
}
return x;
}
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) {
if (rank[rootX] > rank[rootY]) {
root[rootY] = rootX;
} else if (rank[rootX] < rank[rootY]) {
root[rootX] = rootY;
} else {
root[rootY] = rootX;
rank[rootX] += 1;
}
}
}
public boolean connected(int x, int y) {
return find(x) == find(y);
}
}
// App.java
// Test Case
public class App {
public static void main(String[] args) throws Exception {
UnionFind uf = new UnionFind(10);
// 1-2-5-6-7 3-8-9 4
uf.union(1, 2);
uf.union(2, 5);
uf.union(5, 6);
uf.union(6, 7);
uf.union(3, 8);
uf.union(8, 9);
System.out.println(uf.connected(1, 5)); // true
System.out.println(uf.connected(5, 7)); // true
System.out.println(uf.connected(4, 9)); // false
// 1-2-5-6-7 3-8-9-4
uf.union(9, 4);
System.out.println(uf.connected(4, 9)); // true
}
}'꼬꼬마 개발자 노트 > Coding Problems' 카테고리의 다른 글
| Leetcode - Graph (0) | 2022.01.26 |
|---|---|
| Graph -chaper 1(2) (0) | 2022.01.20 |
| Graph - overview (0) | 2022.01.18 |
| Arrays-chapter6 (0) | 2022.01.17 |
| Arrays - chapter5 (0) | 2022.01.13 |

